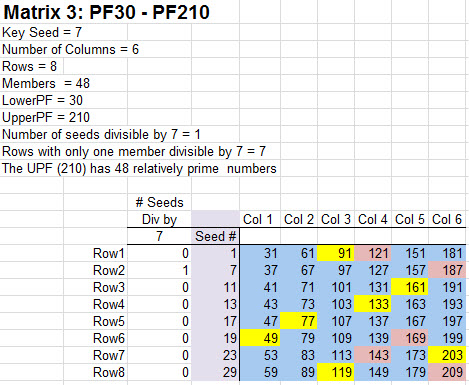
For the creation of Matrix 3, the prior matrix Key Seed number 5 and its multiple 25 have to be removed from the Key Seed list to build the next matrix. All of the primes are in blue squares. Numbers in yellow squares are divisible by the Key Seed number. The pink squares are relatively prime to the upper PF (210) but are themselves not prime. They are divisible by one or more of the seed numbers other than the Key Seed. Rule 3 is that all multiples of the Key Seed have to be removed from the list of seeds to be used in the next matrix.
It is important to make a distinction between the column of seed numbers and the numbers in the matrix. The matrix does not include the seed number column. All of the seed numbers were discovered in a prior matrix and can never be included as part of a new matrix. So in this case there are 48 members of the matrix. The matrix is bounded on the lower side by the lower PF of 30 and the upper PF of 210. Once again you can locate the number pairs which add up to 210 (ex. 1+209, 7+203 etc.) Notice that every number in the matrix can be derived directly by repeatedly adding the lower PF number 30 to the seed numbers. One of the peculiarities that you will notice in Matrix 3 is the presence of one and only one yellow square per row. As it turns out there is one and only one number per row, including the seed numbers, that is divisible by the Key Seed number. I have no proof that this is true but it is clearly obvious and you will find upon inspection of higher matrices that this is indeed true. This leads to an interesting result. The number of numbers in the matrix and seed column divisible by the prime seed is exactly equal to the number of seeds in column 1. This means by removing all of the numbers from both the seed column and the matrix divisible by the Key Seed, the result is equivalent in number to removing the same count of numbers in the seed column itself. This accounts for the computation of the number of members of the matrix by taking the count of members of the prior matrix and multiplying by the Key Seed minus 1. So in this case Matrix 2 had 8 members and the Key Seed in Matrix 3 is 7. We subtract 1 from 7 to get 6 and multiply it by 8 to get 48 which is the exact number of numbers relatively prime to 210 (which is the exact number of members of Matrix 3). This is significant because these are similar but different lists of numbers!